
Here I continue to explore my toy model describing a possible mechanism for the anomalous change in the Earth’s obliquity of the ecliptic from the creation over the period of about 6,000 years. My model does not require rapid changes to occur during the great deluge but that God set in motion a process soon after creation, probably at the Curse, that led to a very disturbed magnetic field and a change in the angle of the tilt of the Earth’s rotation axis. The tilt change was not so fast as it took several thousand years to change by 1.5 degrees, recovered by 3 degrees and then returned to the secular trend over the subsequent several thousand years. If this did in fact occur I would like to understand why it did.
The planet Earth is precessing in its orbit through space. Precessing is the motion of a spinning body where the rotation or spin axis traces out a circle over time. See Fig. 1. The symbol P describes precession and N nutation. Nutation is a small wobble about the spin axis. The Earth’s axis is tilted to the plane of the planets and Sun, known as the ecliptic.

Angular precession frequency (Ω) of the Earth’s rotation axis is the rate of change of the angle Ψ as shown in Fig. 1. This is described by the following equation.
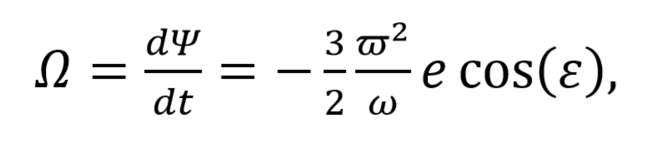
… (1)
where ϖ is the Earth’s angular orbital velocity in its yearly circuit. The Sun’s mass (M) and Earth’s distance (R) from the Sun determines this.

… (2)
where m is the mass of the Earth. But because gravitational mass (right side) and acceleration or inertial mass (left side) are equivalent in nature (by the equivalence principle) the m’s cancel and we get,

radians/sec. … (3)
The parameter ω is the angular rotation velocity of the planet over the 23.9972-hour day with respect to the stars. That is the sidereal day, which is 4 minutes less that the sinodic day which most are familiar with as the 24-hour day from sunset to the following sunset. Therefore ω ≈ 7.2921⨉10-5 radians/sec.
The parameter e is the Earth’s oblateness. Because the Earth is not perfectly spherical but is a spheroid (an ellipsoid of revolution) oblateness (e) can be calculated from the radii at the equator and the poles:

The angle (ε) is the obliquity (angle of tilt) that the Earth’s rotation axis makes with the normal to the plane of the Earth’s orbit (called the ecliptic plane, because it is the plane in which eclipses can occur). Since the equator is inclined to the ecliptic at about 23.435°, the axis therefore describes a cone in space with semi-vertical angle ε = 23.435° at the current time. See Fig. 1.
Using eq. (1) we get rate of precession of the Earth rotation axis due to the Sun of Ω = -16.56 arcsecs/year but about -50 arcsecs/year are measured. The minus sign is because precession is retrograde to the West to East rotation of the planet.
The Moon contributes about double the effect of the Sun so when we add that in we get Ω = dΨ/dt = – 49.67 arcsecs/year, which gives you a precession period of about 26,000 years. That means for the precession angle Ψ to make a full 360° or 2π revolution around the circle shown in Fig. 2. Of course no one has measured a full period of precession.
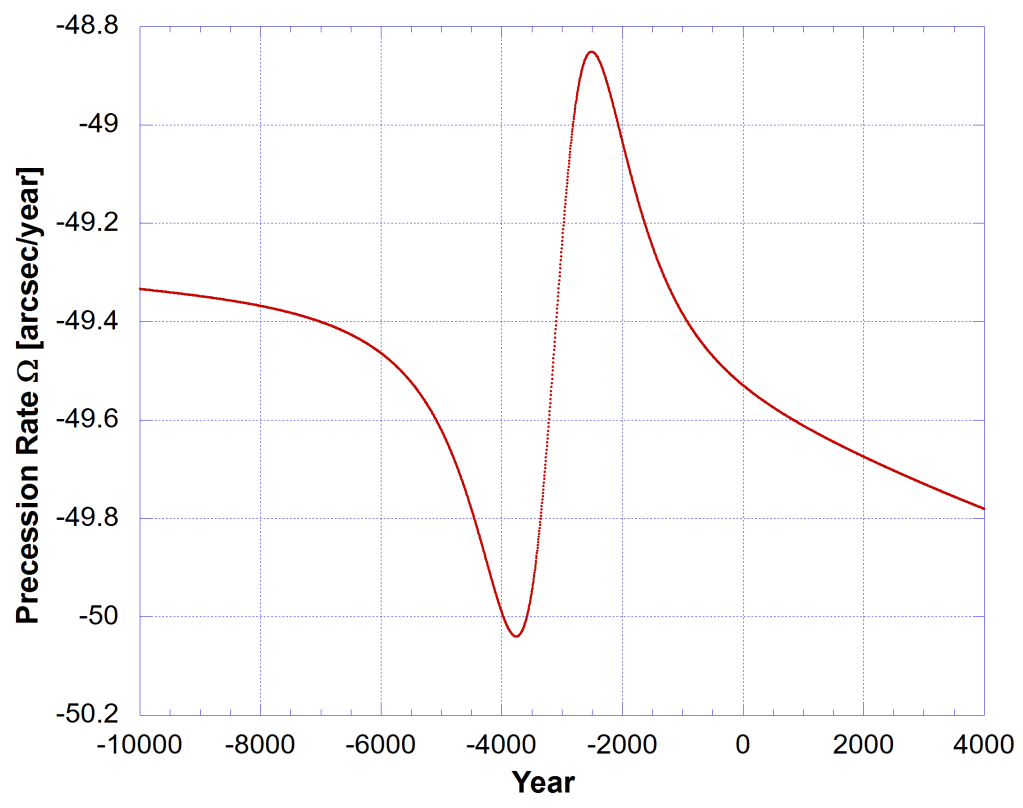
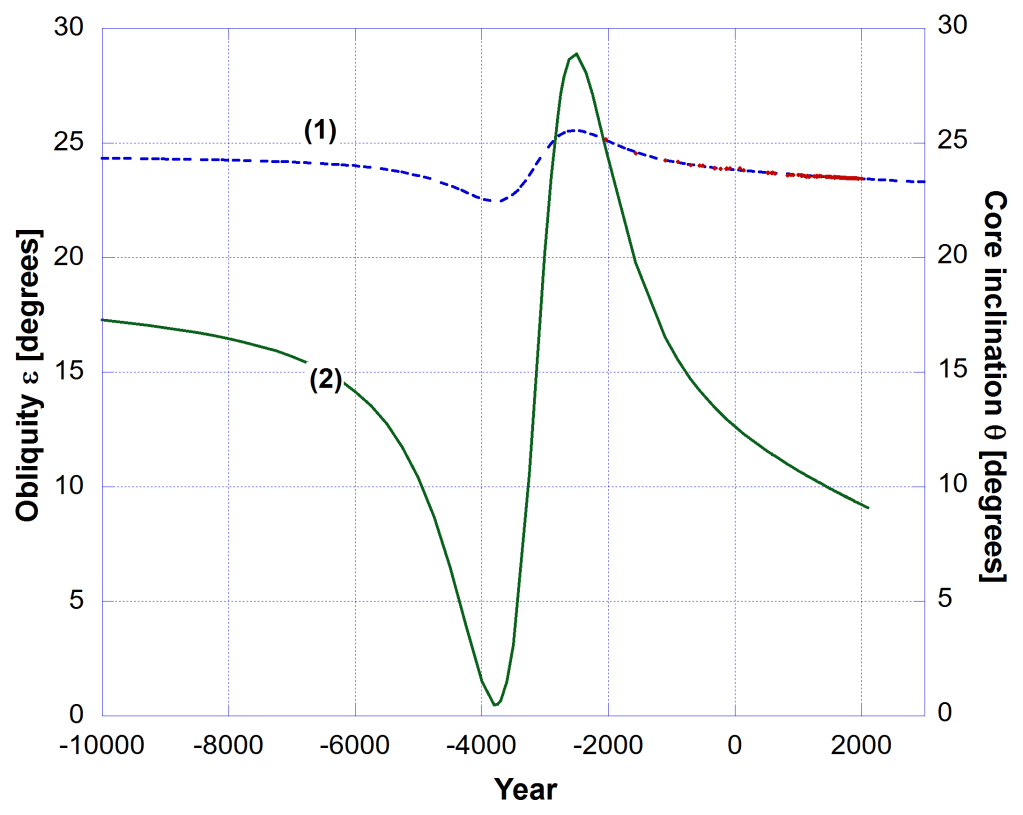
The slight change in the obliquity of the ecliptic (ε) over time has very little effect on the precession rate Ω. It is dependent on the cosine of the angle ε, which changes little over 10,000 years. Based on the gravitational effects of the Sun and Moon (primarily) the secular change in tilt is described by the solid curve (1) in Fig. 3, which is described by what is called Newcomb’s formula. There I used the fifth order polynomial version. However what if something actually happened in my model to change the obliquity of the rotation axis according to the dashed curve (2) in Fig. 2? Then the obliquity deviated by about 1.6 degrees either side of the secular trend.
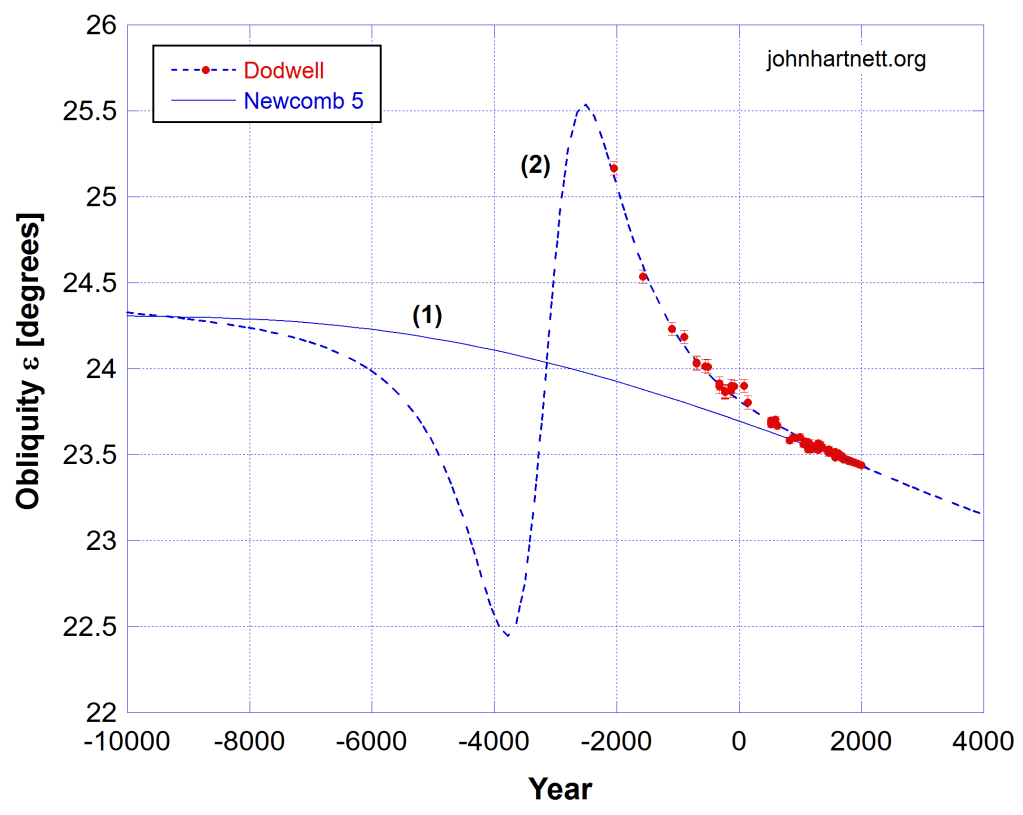
Fig. 2 shows a period greater than the biblical timeline, which was no more than 8,000 years from creation. So even if you truncated the negative axis at -6000 for the time of creation you’ll notice that the perturbation in the obliquity was already underway. The question is, what effect did this perturbation have on the precession rate?
Using eq. (1) I modelled the effect and it is shown in Fig. 3. As you can see it only means a small deviation in the precession rate Ω = dΨ/dt. There is no major disturbance there. The co-ordinate scale is in arcsecs/year, and would vary by only 0.5 arcsecs/year around the mean of -49.5 arcsecs/year. When this is integrated over time to calculate the 360° revolution around the circle of precession the result is still about 26,000 years.
However that modelling did not include adding any additional mass to achieve the disturbance (perturbation) to the obliquity, according to curve (2) in Fig. 2.
The precession of the Earth’s rotation axis results from the fact that the Earth is an oblate spheroid. If it was a perfect sphere no precession would occur. The oblateness results primarily from the angular momentum of our rotating planet, which is plastic and deformable and covered in water. Thus it has a flattening at the poles and a bulging at the equator, not to be confused with the tides, a gravitational effect and described below.
When considering the gravitational acceleration at the surface of the deformable Earth. In the case of the Moon, in an Earth centred frame, the dipole term yields a uniform gravitational acceleration g0 = Gm′/a2 directed towards the Moon. That term therefore describes the major effect of the Moon’s gravitational force, which is to accelerate the Earth as a whole.
The next expansion term, the quadrupole term, is a much smaller term than the gravitational dipole term g0, but it gives rise to tides. See Fig. 4.
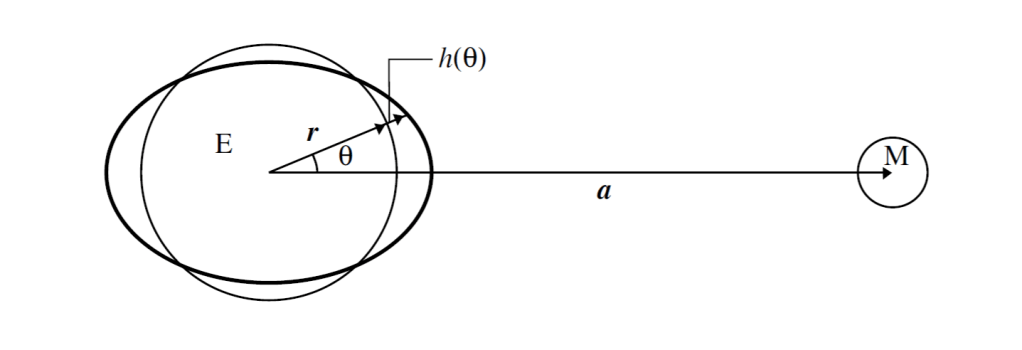
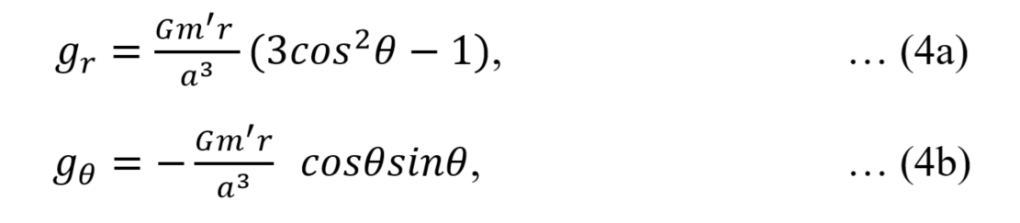
where the mass of the Moon is m’, its distance a, and Earth radius r = average radius + tide height (h(θ)). The distance a is directed towards the Moon with the force in that direction pulling the oceans towards the Moon making high tides. The angle θ between a and r characterises the low tides perpendicular to the Moon direction. The negative sign in eq. (4b) means the force is inwards towards the centre of the Earth.
The effect on the precession rate can be considered via the effect of the Moon. The gravitational moment of the Moon is about twice that of the Sun as mentioned above. This is the only gravitational system in the solar system like that. Another design issue.
The gravitational moments depend on the masses of these bodies and the inverse cube of their distances. That is, for the Moon’s mass m’and distance a and the Sun’s M and distance R we get
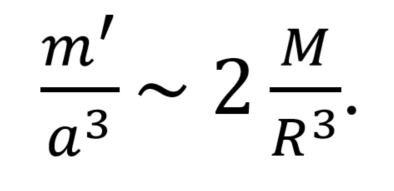
This fact also means that the ocean tides due to the gravitational pull of the Sun and the Moon are of similar magnitude. A calculation yields heights less than a meter. But the actual measured tide heights depend more on the geography of the bays and inlets etc.
Therefore we can conclude that if we were to add additional masses like that of the Moon at the distance of the Moon it would change the rate of precession proportionally but it would create larger tides also in proportion to the added masses.
Some astronomers have suggested that in the long evolutionary past Earth had a second moon which broke up. Though this is not a widely accepted theory, the problem with it is that there would be evidence and we find little to none in orbit at the lunar distance.
So for my toy model to include any extra massive bodies like the Moon it also would need that sort of evidence. If it wasn’t a cylindrically symmetric disk of material it also would exert gravitational forces on the Earth exaggerating the existing tides. And those larger tides would have existed for thousands of years.

A circular disk like Saturn’s rings or the one shown in Fig. 5 would not create extra diurnal tides because the gravitational pull would be the same on all sides. But it would create a larger equatorial bulge like that associated with the rotation of the planet. What influence such a disk leftover from creation week might have?
One could speculate that it added to the global Flood when the disk broke up during that momentous year. The mass of the Earth is 81.3 times the mass of the Moon and 3.66 times the radius of Moon. So if there was an extra Moon-mass worth of water-ice material in such a disk adding it to the Earth’s mass during the Flood would cover the entire surface of the planet to a depth of 129 km. So that is just not a possibility.
A thin icy disk with a mass of 1% of the Moon’s mass would add sufficient water to the Earth to cover it to a depth of 1.3 km, which is more consistent with the global Flood conditions. But such a disk would have caused very insignificant changes in the precession orbit of Earth. However I have yet to model what change in obliquity could be achieved by dumping that mass on the spinning planet.
Now I am inclined to think that another mechanism is possible.
It all began in the core of the planet soon after creation, perhaps at the Curse. The spin axis of the core was set into motion as a reaction/response to the created conditions. That caused it to undergo the 30° total change as shown in curve (2) Fig. 6 as the core axis swung 15° one way, swung back 30° and then returned back 15°. This occurs over about 6,000 years from creation. Read the Fig. 6 timeline beginning in the year -6000 for the creation. The model is described in Can We Know the Year of Noah’s Flood?
So the shift in the core angular momentum vector causes a shift in the Earth’s rotation axis vector and hence the change in tilt. This was necessary for conservation of angular momentum. The time the change in tilt occurred most rapidly in both spin axes is the year of Noah’s Flood. But it was set in motion from the beginning of the creation. The Creator saw the future and set all the “marbles in play”.
Planet Earth is remarkably stable where a 30 degree change in the core inclination only resulted in a corresponding 3 degree change in the obliquity as shown in Fig. 6. This is due to the very large mass and angular momentum of the planet. The Moon and the Sun are also strong stabilizing bodies that have kept the Earth in a stable solar orbit and stable precession. This is all by design.
The main consequence of the changes in the core were in the Earth’s magnetic field. See A Brief History of the Earth’s Magnetic Field and Major Changes in Earth’s Magnetic Dipole Since Creation. Perhaps the initial chaotic magnetic fields in the Earth for the first 4,000 to 5,000 years is further evidence of the initial creation process. Around 1,000 BC the Creator brought order out of chaos and increased the energy to and stabilised the Earth magnetic dipole field. However that has been decaying away over the past 1,000 years.
References
- Tom W. B. Kibble, Frank H. Berkshire, Classical mechanics, 5th Edition, 2004, Imperial College Press.
Related Reading
- Earth’s Magnetic Field: A Shield by Design
- Can Earth’s Magnetic Field Survive for Billions of Years?
- The Mysterious Weakening of Earth’s Magnetic Field Explained
- Earth | A Sphere By Design
- The Sustaining Power of the Creator
- The Physics of Creation | Day 1
- The Physics of Creation | Day 2
- The Physics of Creation | Day 3
- The Physics of Creation | Day 4
- The Physics of the Global Flood
- My Book ‘Physics of Creation’
Free Subscribers
Subscribe to our Newsletters as a Free Subscriber and be notified by email. Just put your email address in the box at the bottom of your screen.
You’ll get an email each time we publish a new article. It is quick and easy to do and totally free. You only need do it once.
Premium Subscribers
Subscribe to our Newsletters as a Premium Subscribers at $5 USD/month or $30 USD/year (you choose).
Paid Premium Subscribers will get exclusive access to certain content I publish. That will only cost you a cup of coffee per month.
This is how you can support my work. I have been publishing this website for 10 years now and up to 2024 I never asked for any support.
Press the button “Premium” on the front page to find a list of Premium content. Thanks so much to all supporters.
At a minimum, please join as a Free Subscriber. It’ll cost you nothing. It may also help me beat the shadow banning of some posts.






Leave a comment