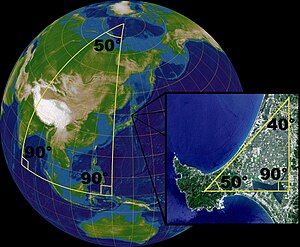
Some very significant properties of the sphere describe a universe designed and created for life. The topological relationship between the sphere’s volume and its surface area impacts our lives in some very important ways, which I describe below.
I’ll try to keep this simple; forgive me if I don’t. However before I get into that consider the globe of the Earth described here through the prophet Isaiah.
21 Have you not known? Have you not heard? Was it not told to you from the beginning? Did you not discern from the foundations of the earth?
22 He abiding over the circle of the earth sees and ones living in it are like grasshoppers; He who stretches the heavens like a curtain, and spreads them like a tent to live in;
23 who [brings] potentates [kings] [to] nothing. He makes judges of the earth as nothing.Isaiah 40:21-23 KJ3
The Hebrew word translated ‘circle’ here is elsewhere translated as circle, circuit and compass in the KJV. Each time it has the meaning of circle in some form. The great circles of the longitudinal lines on the sphere are such circles.

There is no question about who is the Creator in this passage. It is He who sits above the sphere of the surface of the earth and it is He who created the starry heavens and placed them in the firmament. It is He who rules over the kings of the earth.
Over the surface of a sphere up is always vertically above the centre. So for God to be above every point on the surface a sphere, after all He is omnipresent, it is required that we live in a 3 dimensional universe because the sphere is a consequence of that geometry. Then all we need to do is show that the universe has 3 macroscopic spatial dimensions and QED (quod erat demonstrandum).
In Mathematics we can describe a sphere thus.
A sphere (from Greek σφαῖρα, sphaîra) is a geometrical object that is a three-dimensional analogue to a two-dimensional circle. Formally, a sphere is the set of points that are all at the same distance r from a given point in three-dimensional space. That given point is the center of the sphere, and r is the sphere’s radius. The earliest known mentions of spheres appear in the work of the ancient Greek mathematicians.
The sphere is a fundamental object in many fields of mathematics. Spheres and nearly-spherical shapes also appear in nature and industry. Bubbles such as soap bubbles take a spherical shape in equilibrium. The Earth is often approximated as a sphere in geography, and the celestial sphere is an important concept in astronomy. Manufactured items including pressure vessels and most curved mirrors and lenses are based on spheres. Spheres roll smoothly in any direction, so most balls used in sports and toys are spherical, as are ball bearings.
The prophet Isaiah lived in the 8th century B.C. during the period of the Assyrian Empire. This is well before the Greeks, especially Eratosthenes and Aristarchus, who, using their understanding of the sphere measured the diameter of the planet Earth, the Moon and the Sun and their distances, around 200 B.C. to 300 B.C.
The Greek astronomer Aristarchus of Samos (310 B.C. to 230 B.C.) was the first to measure the distance to the Sun. He used the phases of the Moon and Lunar and Solar eclipses to measure the sizes and distances of the Sun and the Moon. He used the diameter of the Earth by Eratosthenes of Cyrene (c. 276 B.C. – c. 195/194 B.C.) to do so.
Mathematical Universe
Their results depend on the logical assumption that we live in a 3-dimensional universe. However, mathematically we can describe the properties of an n-ball in a Euclidean space with an arbitrary number of dimensions n.
The following except from a Wikipedia article describes the mathematical properties of a sphere in a space with n dimensions.

Yes, I know that looks complex. It isn’t really. But if I give you a few examples it will be come clearer.
First we must realise that this is mathematics and that is a language describing mathematical constructs. They don’t automatically apply to the real world. We observe the real world, the physical universe, to determine which is applicable.
We all have experience of a 3D ball, also of an approximation to a 2D ball. The latter is a disk like a pizza tray. But to be accurate it would have to have zero thickness, so therefore I wrote ‘an approximation’.
A 2-ball is also called a 1-sphere because the sphere is mathematically the surface, not the volume inside.
A 1-sphere of radius r is described by surface area (or circumference) S1 = 2πr and an inside volume V2 = πr2. That is the ideal disk of zero thickness in a 2 dimensional space. Think of it as a flat circular disk.
A 2-sphere of radius r is described by surface area S2 = 4πr2 and an inside volume V3 = 4/3πr3. That is the standard sphere in a 3 dimensional space as shown in the image above. The inside volume is called a 3-ball.
One more example. A 3-sphere of radius r is described by surface area S3 = 2π2r3 and an inside volume V4 = π2/2r4. That is a 4-ball, in a 4 dimensional space.
The surface area of the 4-ball is a 3D volume. But because our minds operate in a 3D space we cannot visualise a 4D ball in a 4D space. This should tell us something already.
The 3-sphere in a 4D space is often referred to as a hypersphere. But the term may be generalised to any (n-1)-sphere in an n-dimensional hyperspace, where n > 0. The properties of a (n-1)-sphere Sn-1 = An-1 and a n-ball Vn are listed above for unit radius r = 1.
Physical Universe
What is the correct mathematical description for the actual physical universe we live in? That is a good question.
Even though in the above n is a real integer, i.e.1, 2, 3 etc, it is not mathematically limited to those numbers. The number of spatial dimensions n could also be a complex number z = a+j.b, where j = square root (-1).
Mathematically there is no natural reason for the universe to have exactly 3 spatial dimensions, only length, width and height. Why should it not have dimensions, for example, z = 3.1 or z = 3.1 + j2.1 (a complex number)?
Theoretical physicists have developed a host of theories in an effort to better describe the outcomes of experiments especially in particle physics and astrophysics. Some theories, like string theory or M-theory, incorporate extra spatial dimensions, but in all cases they are compactified. That is, the extra dimensions are rolled up inside some elementary particles.
The reason for this is that no experiments that we have done locally (within the solar system) allow for any more or less than exactly 3 spatial dimensions. So if the theory has 9 dimensions then 6 of them must be compactified. This is because of what we measure in actual experiments.
Particle physics deals with sub-atomic particles and there may be room for higher dimensions there but I personally do not think so. All experiments on supersymmetry theory (SUSY) have failed to yield the promised results. That should be the end of string theory.
Electromagnetics
The way light, or any electromagnetic radiation, propagates through space depends the number of dimensions (n) of that space.
Imagine a wavefront of light from the Sun (S) below. The intensity (I) of light received over a finite area decreases from its initial value (I0) as a function of the distance, 1/r2.
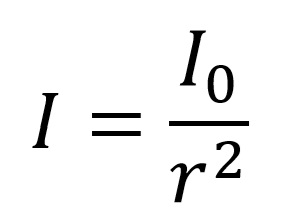
The intensity (or irradiance) decreases proportionally with the square of the distance r. Or we could say the area to capture the same number of photons increases as r2. This is the well known and established law, the inverse Law of Illumination.

Over the whole surface area S2 = 4πr2 as radius r from the Sun grows, the area grows but the total energy in the wavefront (which includes all photons) is constant. Therefore over a fixed area, for example the lens of a camera or the eye of the observer, the number of photons arriving decreases as r2 increases. This means that in a 3D space a 2-sphere describes exactly what we measure in such experiments.
Lab measurements have been routinely done to quantify the value of n here by assuming it is a non-integer value. All such experiments are consistent with (n-1) = 2, within experimental error. This is a basic educational experiment for first year physics students at university.
Electrostatics
The force (F) of attraction or repulsion between two electrically charged particles (q1, q2), in addition to being directly proportional to the product of the electric charges, is inversely proportional to the square of the distance r between them; this is known as Coulomb’s law, shown below where ke is a constant.
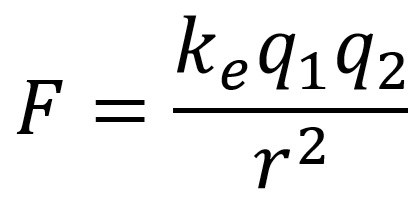
This is another inverse square law based on exactly the same dimensionality of the universe as described above.
Experiments have been done with extreme precision and they have found the deviation of the exponent (n-1) from exactly 2 is less than one part in 1015. This is extremely solid evidence for an n = 3 dimensional universe. Both 2D and 4D universes are excluded, but so are all universes where n or z is not exactly 3.
There are many inverse square laws related to the number of spatial dimensions in the universe. One more is worth considering.
Gravitation
The Newtonian gravitational force law is totally analogous to the electrostatic force law and is described by the famous equation,

where G is Newton’s constant.
Precision gravitational force experiments to test the value of the exponent (n-1) or its deviation from 2 are very difficult. They are nothing like the precision achieved in the electrostatic experiments but still about 1 part in 10 has been achieved. This was done over a distance of only a few millimetres.
Again the gravitational force law requires a universe of exactly 3 spatial dimensions. It certainly cannot be n = 3.1 or 2.9, or a complex value of z = 3.1 + j2.1 or something like that.
Design Implications
Related to the gravitational force law is the gravitational potential energy field, which decreases as a function of distance r from a central mass. Imagine it like a well with the mass at the centre. All objects fall into that well and the force on them is the gravitational force. If the objects are moving quickly enough they will orbit the central mass. But if not, they will coalesce into a spherical blob. That blob must become spherical because the force at distance r from the centre is equal everywhere on the spherical surface.
All points on that surface are at the same gravitational potential. This is the geoid and is related to the science of geodesy (explained in this video).
All celestial bodies greater than about 100 km diameter are spherical. This is because of those gravitational forces. The force of a planet’s gravity pulls equally from all sides until the surface is all at the same gravitational potential.
In a 3D universe a spherical mass is the natural result. Think of it as the most stable matter configuration. It is the reason the oceans all sit on the same gravitational potential surface called the geoid. It is slightly oblate due to the spin of the planet but still the ocean’s surface is at the geoid.
However if the universe was 2 dimensional, matter could not form into a sphere but only into a disk, which is not what we observe in the universe. And if the universe was 4 dimensional, it would be unimaginable.
At the time of the creation God said that on the first day the earth started out as just water. And it was initially without form.
2 The earth was without form and void, and darkness was over the face of the deep. And the Spirit of God was hovering [brooding] over the face of the waters.
Genesis 1:2 ESV
From the Hebrew word translated ‘deep’ implies an abyss (as a surging mass of water). God’s Spirit was hovering, brooding over and gave energy to the water. Because energy implies motion, I interpret this to mean both electromagnetic and gravitational energy. Physics does not know why gravitational mass is equal to inertial mass. It is a big mystery of the universe. Both were created at this moment.
Once the water started gravitating it would all form into a massive sphere with an equal gravitational potential surface. This was the start of the solar system. Then on the fourth day of creation, God formed the rest of the planets from this water.
Of course He created the Sun that day too, which formed into a massive ball of self-gravitating mass. Every aspect of creation, including all the stars and galaxies, are largely spherical in nature. There are non-spherical galaxies, that are spirals, but even they have large spherical cores.
The 3D nature of the earth means it is in a stable gravitational potential well. As explained in It Was No Accident: All Forms of Energy Were Provided by the Creator this results in various providential sources of energy for the inhabitants of the planet.
An evolutionist who denies the Creator might just say that these properties of the sphere seen in the creation are just the product of the accidentally provides laws of physics of the universe that came out of some big bang. That is, they are acknowledging the anthropic laws but as an accident and denying the Creator.
There are a myriad of properties of matter in the Earth’s gravitational field that we take for granted. Air pressure is stratified and forms a shell and a shield around the spherical planet. Imagine a irregular shaped planet where the potential energy surface is chaotic and unstable. That would not be conducive to life.
The inverse square law of illumination is also a design feature. It keeps the stars from burning us. Each star is a sun, some incredibly massive in size. Their distances mean their irradiance is extremely diluted by the time the photons get to Earth.
Our spherical planet is made oblate by its rotation. This rotating effect equilibrates the heating effect of solar irradiance on the 24-hour day/night cycle. The planet’s rotation on its central spin axis is a property of a sphere.
Consider the planet Mercury which is tidally locked to the Sun. It always presents the same side to the Sun. The planet is much closer and with no atmosphere and thus hotter than Earth but the tidal locking means roasting temperatures on the Sun side.
Earth’s distance from the Sun puts it into the habitable zone in the solar system, where the temperature is suitable for life and water is in its liquid state. With many thousands of planets now being found around other stars very few are in habitable zones, and very few are of a suitable mass to produce a gravitational field consistent with life as we know it.
The orbital motion of the planets in the solar system set up this habitable zone. The planets’ orbital positions are due to a combination of the gravitational forces on the planets and their motion to keep them in stable orbits, among other factors. So this also relates back to that inverse square law of gravitation, which in turn comes from the physics of the 2-sphere, which comes from a 3-dimensional universe.
Related Reading
- 6-Day Creation of the Universe
- It Was No Accident: All Forms of Energy Were Provided by the Creator
- Why is the Night Sky Black?
- Life on Earth 2.0—Really?
- Life in the Universe is the Ultimate Miracle
- Evidence Against a Flat Earth: Solar Eclipse Shadows Exmouth, Western Australia
- Job 38 and a Flat Earth
Follow me
- Telegram.org: @GideonHartnett
- X (Twitter): @gideon195203

To be notified by email put your email address in the box at the bottom of your screen. You’ll get an email each time we publish a new article.

Click this image to make a secure Donation (Stripe) !






One response to “Earth | A Sphere By Design”
Good point about gravitational potential:
“That blob must become spherical because the force at distance r from the centre is equal everywhere on the spherical surface.“
If that doesn’t convince someone who thinks the Earth is flat, then ask him while he is watching the Sun rise in the East to call someone far away to ask that far away person where he sees the Sun. That far away person may be so far away that he is watching the Sun set in the West.
If that doesn’t convince him, then show him a travel video of people on a cruise around Antarctica.
LikeLike